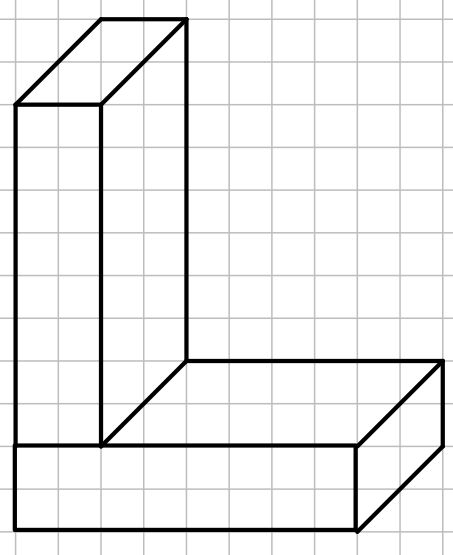
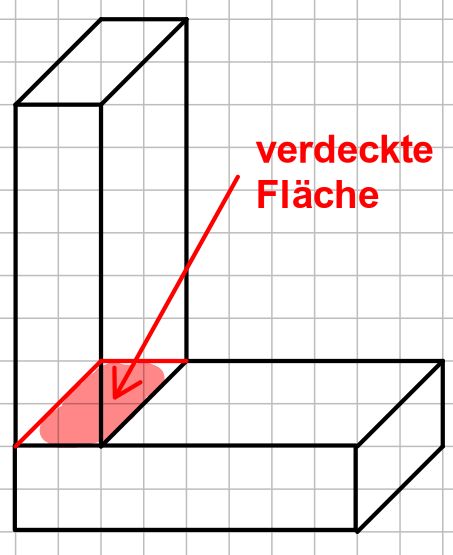Warum kann man für einen Körper aus zwei Quadern nicht einfach die Oberfläche bestimmen, in dem man die Oberfläche der beiden Quader addiert? Weil ein Teil der ursprünglichen Quaderoberfläche nicht mehr zur Gesamtoberfläche gehört (verdeckt wird).	2m = 120sek : 30 = 4sek · 2 = 8sek Was ist daran falsch? Hier werden mehrere Rechnungen in einer geschrieben. Es gilt nicht das 120:30 = 4· 2 ist.  Bitte in drei Rechnungen aufschreiben: 2m = 120sek 120sek : 30 = 4sek 4sek · 2 = 8sek	Ein Bruch (z.B. \(\frac{30}{4}\)) ist auch eine ... - Aufgabe Ein Bruch ist auch eine Divisions-Aufgabe (Quotient, Geteilt-Aufgabe) \(\frac{30}{4}=30: 4\)
Ein Liter (1 l) ist gleich 1 ___³  Ein _________ (1 __) ist gleich 1dm³	Ein _________ (1 __) ist gleich 1dm³ Ein Liter (1 l) ist gleich 1 ___³	Ein _________ (1 __) ist gleich 1cm³ Ein Milliliter (1 ml) ist gleich 1 ___³
Ein Milliliter (1 ml) ist gleich 1 ___³  Ein _________ (1 __) ist gleich 1cm³	Lässt sich jeder Bruch am Zahlenstrahl eintragen? Wenn ja wie? Ja - jeder Bruch kann am Zahlenstrahl eingetragen werden. Gegebenenfalls kürzt oder erweitert man den Bruch auf einen Nenner der zu den Strichen am Zahlenstrahl passt und trägt ihn dann so ein, dass man zunächst schaut, zwischen welchen beiden natürlichen Zahlen er stehen muss und dann dazwischen so viele Stücke malt, wie zum Nenner passen. Dann kann man die richtige Stelle finden.	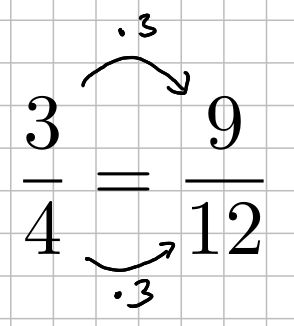Man erweitert einen Bruch, indem man … … den Nenner und den Zähler mit der gleichen Zahl mutlipliziert
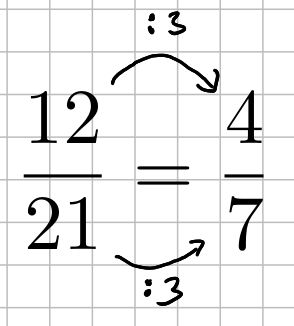Man kürzt einen Bruch, indem man … Den Nenner und den Zähler jeweils durch die gleiche Zahl teilt.	Nenne Beispiele: Was sind Körper mit geraden Kanten und Flächen bzw. Körper mit gerkümmten Kanten oder Flächen? Mit gekrümmten Kanten und Flächen haben wir z.B. den Zylinder, Kugel, Halbkugel	Nenne mindestens einen Bruch der am Zahlenstrahl zwischen den natürlichen Zahlen 0 und 1 liegt z.B. \(\frac{1}{2}\) - der liegt immer genau in der Mitte, weil es die Hälfte von 1 ist. ebenso \(\frac{7}{9},\frac{2}{3},\frac{3}{4},\frac{127}{183},\dots\) (immer ist der Zähler kleiner als der Nenner) Erklärung: Alle Brüche bei denen der Zähler kleiner als der Nenner (und größer als 0) ist, liegen zwischen 0 und 1,
Nenne mindestens einen Bruch der zwischen den Zahlen 2 und 3 liegt z.B. \(\frac{12}{5}\), denn der Zähler 12 ist größer als 2·5=10 und kleiner als 3·5=15 ebenso: \(\frac{7}{3}, \frac{17}{7},\frac{127}{50},\dots\) (immer ist der Zähler mehr als doppelt so groß wie der Nenner und weniger ...) Erklärung: Wenn der Zähler mehr als zweimal so groß ist wie der Nenner ist der Bruch größer als 2 und wenn der Zähler weniger als dreimal so groß ist wie der Nenner ist der Bruch kleiner als 3 - also liegt er zwischen 2 und 3	Warum heißt der Zähler, Zähler? Weil er die Anzahl der Stammbrüche zählt. 3/7 sind drei mal so viel wie 1/7	Warum ist \(\frac{1}{4}+\frac{1}{8}\) nicht gleich \(\frac{1}{3}\)? Im Bild sind  \(\frac{1}{4}+\frac{1}{8} = \frac{3}{8}\) gefärbt. Wenn man nochmal den gleichen Anteil färbt bleibt nur ein Viertel übrig, also ist der gefärbte Anteil mehr als ein Drittel. (Andere Erklärungen sind auch möglich!)
Warum ändert sich beim Erweitern oder Kürzen der Wert des Bruches nicht? Weil sich zwar die Anzahl der Stücke (Zähler) verändert aber die Stücke/Teile (Nenner) in gleichem Maße kleiner oder größer werden. Wenn ich einen Bruch mit 2 erweitere, verdoppelt sich die Anzahl der Stücke aber die Stücke sind nur halb so groß. 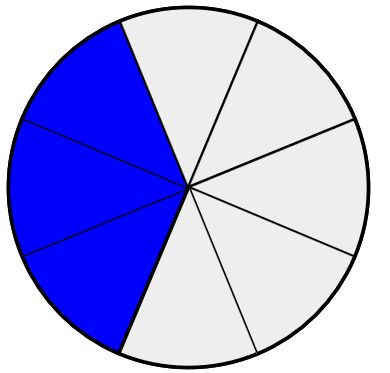 \(\frac{3}{8}\)  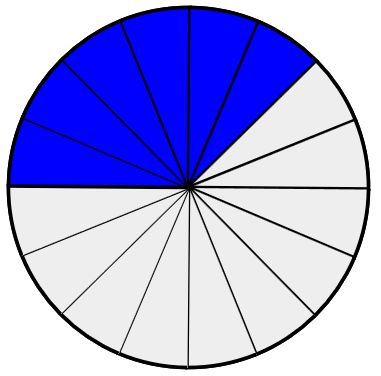 \(\frac{6}{16}\)	Was hilft, wenn man sich bei der Umrechnung von Einheiten unsicher ist? (z.B. 7,57dm³ in mm³ umrechnen)?	Was ist 1hl ? 1hl = 1 Hektoliter = 100l
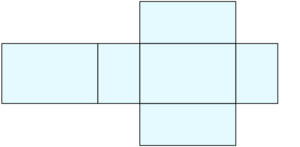
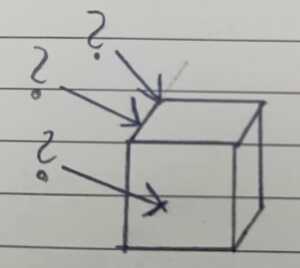
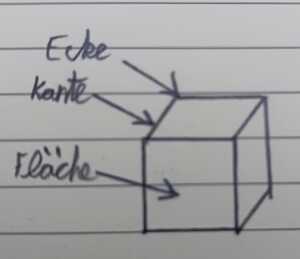
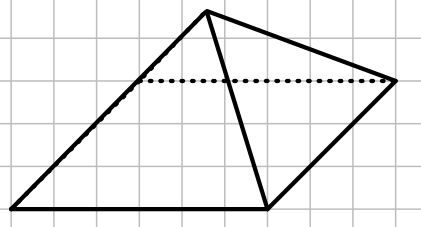
Was ist der Zähler, was der Nenner eines Bruches? Der Zähler steht über dem Bruchstrich, der Nenner darunter. \(\frac{\text{Zähler}}{\text{Nenner}}\)	Wie heißt das folgende Objekt? Was ist ein Körpernetz?	Was ist ein Körpernetz? Wie heißt das folgende Objekt?
Was ist ein Quader? Ein Quader ist der Körper der aussieht wie ein Schachtel mit Länge, Höhe und Breite.  Ein Würfel ist auch einer von vielen Quadern	Was ist ein Stammbruch? Ein Bruch mit dem Zähler 1, z.B. \(\frac{1}{9}\)	Was ist ein unechter Bruch? Ein Bruch bei dem der Zähler größer oder gleich dem Nenner ist
Was sind \(\frac{3}{4} \text{ von } 12kg\) ? Das sind 9kg, denn 1/4 sind 3kg	Was sind \(\frac{3}{5}\) ?	Was stellt man sich unter Brüchen am Zahlenstrahl vor?
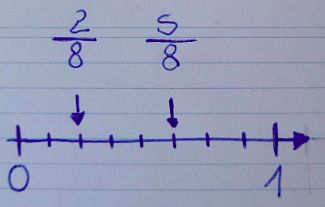
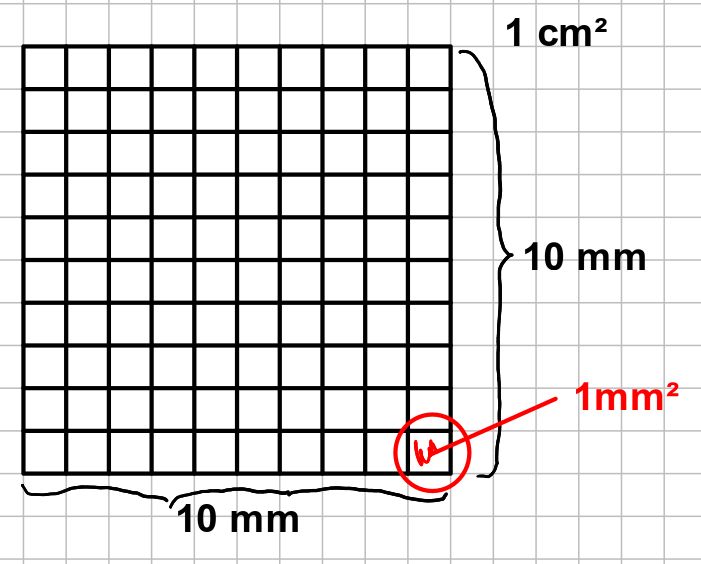
Welche Eigenschaft hat ein Bruch bei dem der Zähler größer als der Nenner ist? Er ist größer als 1 (mehr als ein Ganzes) Man nennt ihn unechten Bruch	Welchen Umrechnungsfaktor verwendet man bei Flächen und warum? Der Umrechnungsfaktor ist 100, denn jedes Quadrat einer Einheit besteht aus 100 Quadraten der nächstkleineren Einheit 1cm² besteht aus 100 mm²	Wenn ich zwei Brüche vergleichen soll (schauen welcher Bruch größer ist), dann ... könnte ich die Brüche zeichnen Wenn der Nenner gleich ist brauche ich nur die Zähler (oben) zu vergleichen Sonst: Ich erweitere auf den gleichen Nenner und vergleiche dann
Wie berechnet man \(1/7\) von 28 ? Man teilt 28 durch 7 und erhält somit den siebten Teil von 28	Wie berechnet man \(\frac{3}{7}\) von 28? Man berechnet zunächst \(\frac{1}{7}\)und multipliziert das dann mit 3	Wie berechnet man das Volumen eines Quaders? Volumen ist gleich Länge mal Breite mal Höhe V = a·b·c
Wie berechnet man das Volumen eines Würfels? V = a³ = a·a·a weil alle Kanten gleich lang sind. Länge=Breite=Höhe	Wie berechnet man die Oberfläche eines Würfels? O = 6 · a · a = 6 a² Sechs mal die Fläche einer quadratischen Seite	Wie groß ist der Umrechnungsfaktor bei Volumen und warum? 1000, denn eine Einheit einer Größe (z.B. cm³) enthält 1000 Würfelchen der nächstkleineren Einheit (mm³)
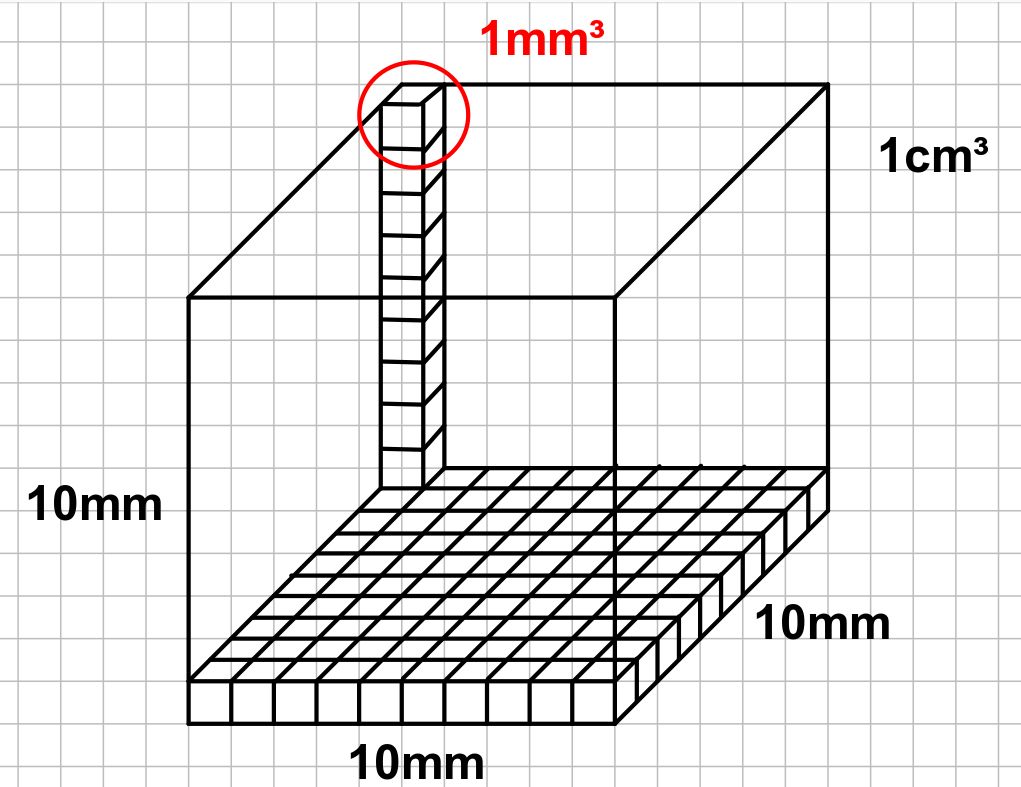
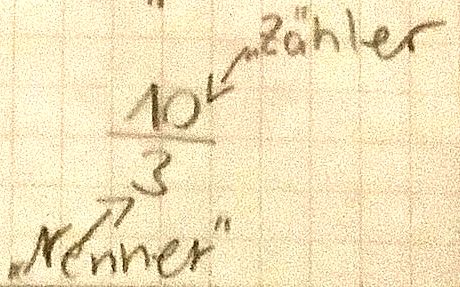
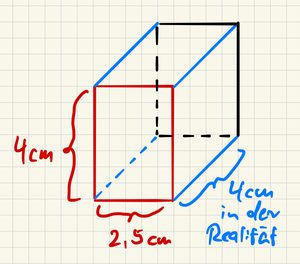
Wie heißen die Einheiten für Volumen? mm³ - cm³ - dm³ - m³ - km³ , Liter(l) und Milliliter (ml)   Kubikmillimeter, Kubikzentimeter, ... 1 l = 1dm³ und 1 ml = 1cm³	Wie heißt die Zahl oben und die Zahl unten? Zähler (oben) und Nenner (unten)	Wie malt man das Schrägbild eines Körpers? Man zeichnet die Vorderseite in den gegebenen Längen und für die schräg nach hinten verlaufenden Linien zeichnet man für 1cm in der Realität eine Kästchendiagonale in das Bild.
Wie nennt man die ? bei Körpern ?	Wie rechne ich zwei Brüche zusammen, wenn sie nicht au dem gleichen "Nenner" sind? Ich bringe die "Nenner" auf den gleichen Stand (durch Erweitern) und dann kann ich die Zähler addieren. \(\frac{2}{3} + \frac{1}{4} = \frac{8}{12}+\frac{3}{12}=\frac{11}{12}\)	Wie schreibt man den gefärbten Anteil als Bruch? Man zählt erst einmal aus wie vielen Kästchen das ganze besteht und dann wie viele Kästchen gefärbt sind. Bruch: \(\frac{10}{24}=\frac{5}{12}\)
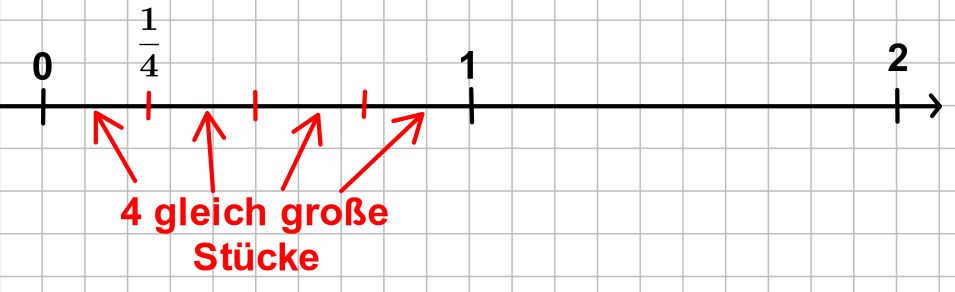
Wie trägt man den Bruch \(\frac14\) auf einem Zahlenstrahl von 0-1-2 ein? Der Bruch \(\frac14\) entspricht einem Viertel der Länge von 1, d.h. man betrachtet die Strecke von 0 bis 1 und teilt sie in vier gleich große Stücke. \(\frac14\)liegt genau zwischen dem ersten und dem zweiten Stück.	Wie vergleicht man zwei Brüche? z.B. \(\frac{3}{5}\) und \(\frac{5}{8}\) Man erweitert oder kürzt sie so, dass die Nenner (unten) gleich sind. Dann ist der Bruch mit dem größeren Zähler größer. Im Beispiel erweitert man z.B. auf 40 = 5·8 \(\frac{3}{5}=\frac{24}{40}\) und \(\frac{5}{8}=\frac{25}{40}\) also ist \(\frac{5}{8}\) der größere Bruch, da 25 Vierzigstel mehr sind als 24 Vierzigstel.	Wie zeichnet man den Bruch \(\frac25\) auf einen Zahlenstrahl? Man muss von 0-1 (auf dem Zahlenstrahl) in 5 Teile teilen. So weiß man, wie groß \(\frac15\) ist. Da man \(\frac25\) einzeichnen muss, zeichnet man sie beim Ende von zwei Strichen die so groß wie \(\frac15\) sind ein.
Woraus besteht die Oberfläche dieser Pyramide? Aus einem Rechteck (Quadrat) und vier Dreiecken.	Woraus besteht die Oberfläche dieses Prismas? Aus zwei Dreiecken und 3 Rechtecken	Woraus besteht die Oberfläche eines Zylinders? Aus zwei Kreisen und einem Rechteck (der Mantelfläche)